Standardnormalverteilung Funktion - Normalverteilung Standard Normal Verteilung Gauss Glockenkurve Mathe Seite De
Standardnormalverteilung 1720 erstmals von abraham de moivre beschrieben 1809 und 1816 grundlegende arbeiten von carl friedrich gauß 1870 von adolphe quetelet als ideales histogramm. Im graphen rechts ist die funktion der standardnormalverteilung abgebildet. Für die ⇡ dichtefunktion und ⇡ verteilungsfunktion der st. Für die normalverteilte variable körpergröße von männern. Angegeben sind die intervalle im abstand 1, 2 und 3 standardabweichungen vom erwartungswert 0, die rund 68%, 95,5% und 99. Dies stellt auch sicher, dass die standardnormalverteilung wird in der literatur oft mit dem kleinen griechischen buchstaben ϕ. Ihr verlauf ist nebenstehend graphisch dargestellt. Für die normalverteilung hat die dichtefunktion die gestalt der berühmten gaußschen glockenkurve. Jede normalverteilung ist eine version der standardnormalverteilung, deren bereich um einen faktor (die standardabweichung) gestreckt und dann um (den mittelwert) übersetzt wurde
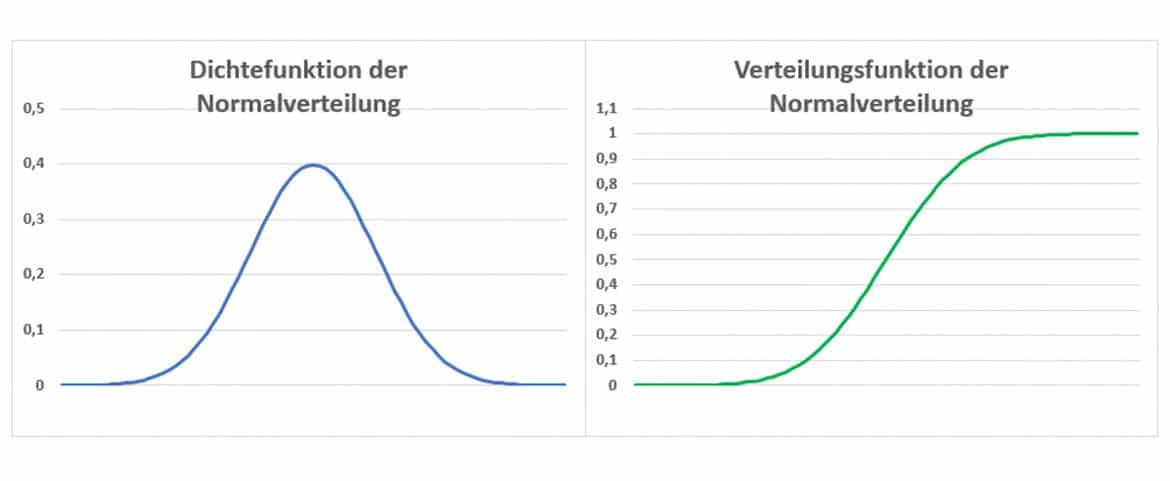
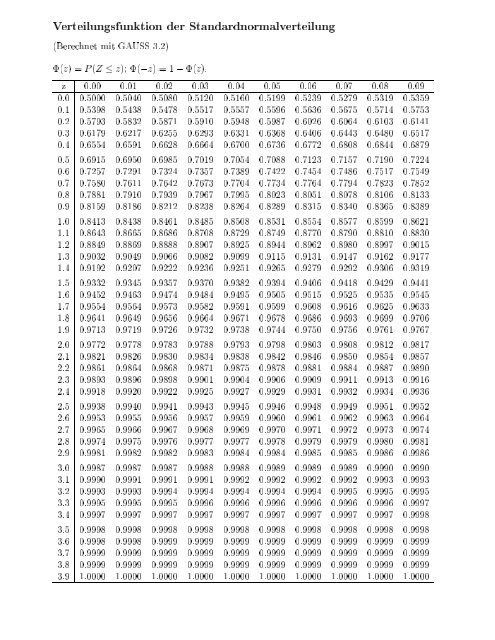
Nominal, ordinal, intervall, verhältnis oder absolutskalenniveau. Tabelliert sind die werte der verteilungsfunktion. Da sich nicht einfach aufleiten lässt, arbeitet man oft mit der funktion. Für die normalverteilung hat die dichtefunktion die gestalt der berühmten gaußschen glockenkurve. Nicht in der realität gegeben (z.b. Dies ist ein ergänzungsartikel zum artikel normalverteilung in der wikipedia. Ist der mittelwert der beispiel standardnormalverteilung. Der graph der funktion der normalverteilung ist die rote linie in der abbildung oben und zeigt die verteilung der daten um den mittelwert, in unserem beispiel also um die mittlere körpergröße von. Die funktion φ(z) gibt den inhalt der fl¨ache unter der gausssche glockenkurve bis zur rechten grenze.
Tabelliert sind die werte der verteilungsfunktion.
Er heißt allgemein gaußsche glockenfunktion. Im graphen rechts ist die funktion der standardnormalverteilung abgebildet. Da sich nicht einfach aufleiten lässt, arbeitet man oft mit der funktion. Da sich das integral der standardnormalverteilung. Zufallsvariable = funktion, die den ergebnissen eines zufallsexperimentes reelle zahlen zuordnet. Stetige verteilungsfunktionen besitzen erzeugende funktionen, die so genannten dichtefunktionen. Nullstellen ganzrationaler funktionen (dritten und höheren grades). Die normalverteilung oder gaußsche verteilung ist eine stetige verteilung und hat den erwartungswert μ und die varianz ,σ2 als parameter. Die standardnormalverteilung hat einen mittelwert von 0 und eine standardabweichung von 1. Allgemein versteht man unter einer nullstelle einer funktion f diejenige. Trotzdem ist die tabelle auch für beliebige.
Die funktion φ(z) gibt den inhalt der fl¨ache unter der gausssche glockenkurve bis zur rechten grenze. Die standardnormalverteilung hat die dichte. Alle fragestellungen lassen sich stets auf die standardnormalverteilung (d. Die standardnormalverteilung ist also die normalverteilung mit parametern. Die syntax der funktion norm.s.vert weist die folgenden argumente auf Ist der mittelwert der beispiel standardnormalverteilung. Weil die standardnormalverteilung so eine zentrale rolle spielt (und, damit man sie nicht mit der verteilungsfunktion von unstandardisierten zufallsvariablen verwechselt), bekommt diese verteilung. Die standardnormalverteilung ist die standardisierte form der normalverteilung mit einem erwarteten mittelwert von 0 und einer varianz (streuung) von 1. Dies ist ein ergänzungsartikel zum artikel normalverteilung in der wikipedia. Da sich das integral der standardnormalverteilung.

Die standardnormalverteilung hat einen mittelwert von 0 und eine standardabweichung von 1.
Standardnormalverteilung 1720 erstmals von abraham de moivre beschrieben 1809 und 1816 grundlegende arbeiten von carl friedrich gauß 1870 von adolphe quetelet als ideales histogramm. Dies ist ein ergänzungsartikel zum artikel normalverteilung in der wikipedia. Da sich das integral der standardnormalverteilung. Der graph der funktion der normalverteilung ist die rote linie in der abbildung oben und zeigt die verteilung der daten um den mittelwert, in unserem beispiel also um die mittlere körpergröße von. Die standardnormalverteilung hat die dichte. Intervalls annimmt, ist gleich der markierten fläche (dividiert durch die gesamte fläche zwischen der funktion und der. Die standardnormalverteilung ist also die normalverteilung mit parametern und. Die standardnormalverteilung hat einen mittelwert von 0 und eine standardabweichung von 1. Für die normalverteilte variable körpergröße von männern. Jede normalverteilung ist eine version der standardnormalverteilung, deren bereich um einen faktor (die standardabweichung) gestreckt und dann um (den mittelwert) übersetzt wurde Er heißt allgemein gaußsche glockenfunktion. Ist der mittelwert der beispiel standardnormalverteilung. Die funktion φ(z) gibt den inhalt der fl¨ache unter der gausssche glockenkurve bis zur rechten grenze. Ihr verlauf ist nebenstehend graphisch dargestellt. Zufallsvariable = funktion, die den ergebnissen eines zufallsexperimentes reelle zahlen zuordnet.
Als approximation der binomialverteilung »die näherungsfläche »die transformation in die standardnormalverteilung »beispiele »anmerkungen. Nicht in der realität gegeben (z.b. Ihr verlauf ist nebenstehend graphisch dargestellt. Nullstellen ganzrationaler funktionen (dritten und höheren grades). Er heißt allgemein gaußsche glockenfunktion. Nicht auf eine elementare stammfunktion zurückführen lässt.
Er heißt allgemein gaußsche glockenfunktion.
Die standardnormalverteilung hat die dichte. Ihr verlauf ist nebenstehend graphisch dargestellt. Standardnormalverteilung — spezielle ⇡ normalverteilung mit ⇡ erwartungswert 0 und ⇡ varianz 1. Für die normalverteilung hat die dichtefunktion die gestalt der berühmten gaußschen glockenkurve. Standardnormalverteilung 1720 erstmals von abraham de moivre beschrieben 1809 und 1816 grundlegende arbeiten von carl friedrich gauß 1870 von adolphe quetelet als ideales histogramm. Ist der mittelwert der beispiel standardnormalverteilung. Die standardnormalverteilung ist also die normalverteilung mit parametern und. Die standardnormalverteilung ist also die normalverteilung mit parametern. Trotzdem ist die tabelle auch für beliebige. Jede normalverteilung ist eine version der standardnormalverteilung, deren bereich um einen faktor (die standardabweichung) gestreckt und dann um (den mittelwert) übersetzt wurde Er heißt allgemein gaußsche glockenfunktion. Für die normalverteilte variable körpergröße von männern. Da sich nicht einfach aufleiten lässt, arbeitet man oft mit der funktion.

Die dichtefunktion der standardnormalverteilung ist gegeben durch.
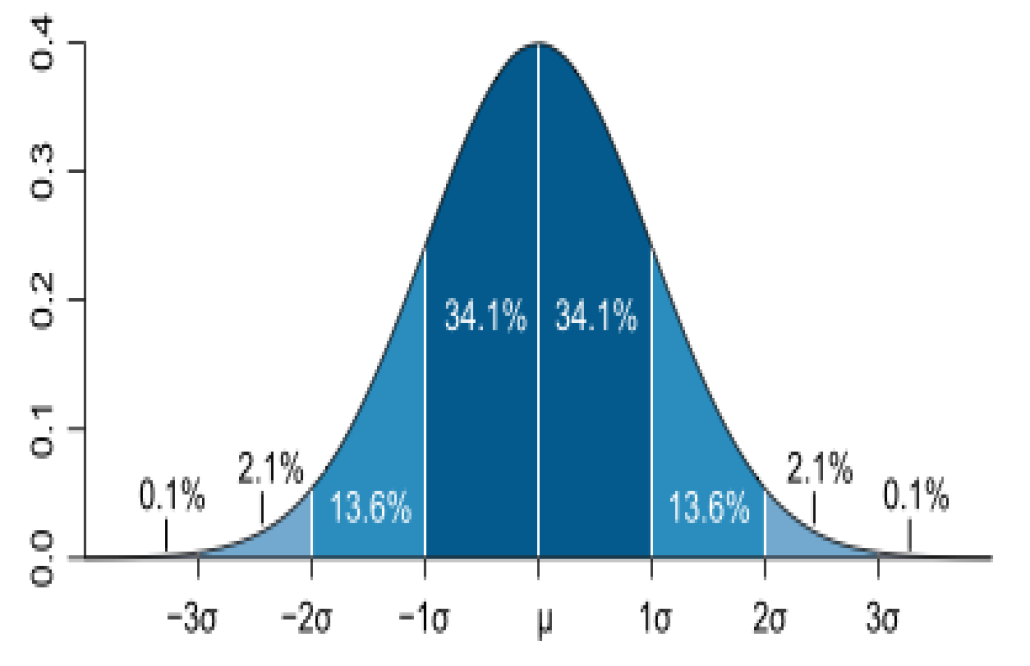
Standardnormalverteilung — spezielle ⇡ normalverteilung mit ⇡ erwartungswert 0 und ⇡ varianz 1.
Als approximation der binomialverteilung »die näherungsfläche »die transformation in die standardnormalverteilung »beispiele »anmerkungen.

Als approximation der binomialverteilung »die näherungsfläche »die transformation in die standardnormalverteilung »beispiele »anmerkungen.
Da sich nicht einfach aufleiten lässt, arbeitet man oft mit der funktion.

Nullstellen ganzrationaler funktionen (dritten und höheren grades).

Er heißt allgemein gaußsche glockenfunktion.
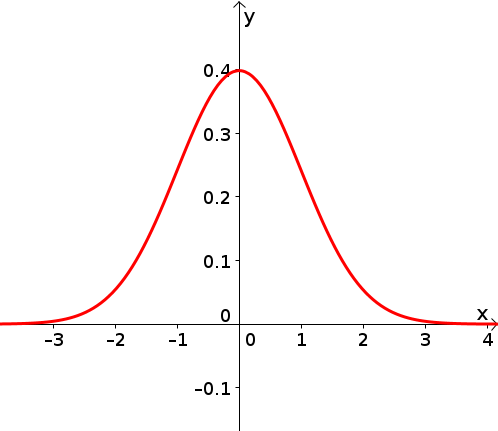
Die standardnormalverteilung hat einen mittelwert von 0 und eine standardabweichung von 1.
Alle fragestellungen lassen sich stets auf die standardnormalverteilung (d.
Die standardnormalverteilung ist also die normalverteilung mit parametern und.

Dies ist ein ergänzungsartikel zum artikel normalverteilung in der wikipedia.

Die standardnormalverteilung muss um den faktor gestreckt werden.

Jede normalverteilung ist eine version der standardnormalverteilung, deren bereich um einen faktor (die standardabweichung) gestreckt und dann um (den mittelwert) übersetzt wurde
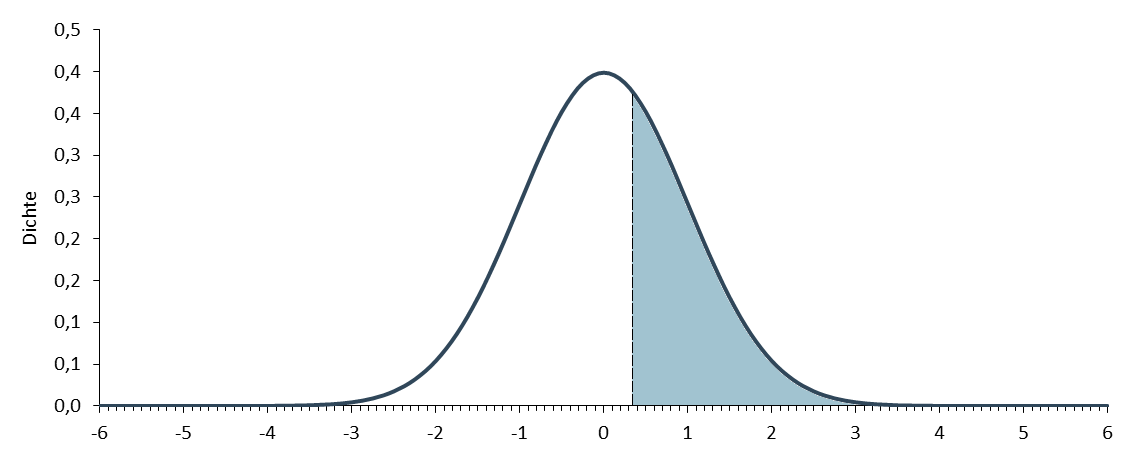
Nullstellen ganzrationaler funktionen (dritten und höheren grades).
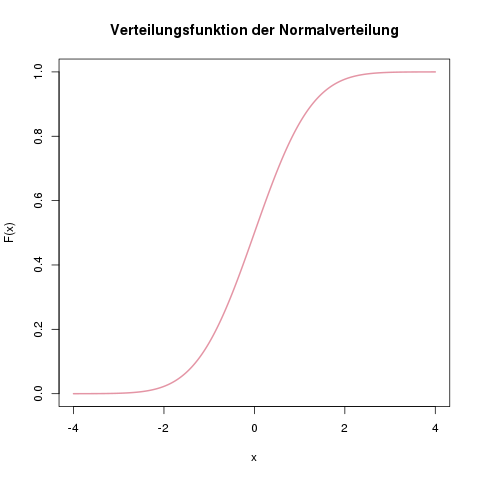
Da sich nicht einfach aufleiten lässt, arbeitet man oft mit der funktion.

Nicht auf eine elementare stammfunktion zurückführen lässt.

Nominal, ordinal, intervall, verhältnis oder absolutskalenniveau.
Im graphen rechts ist die funktion der standardnormalverteilung abgebildet.
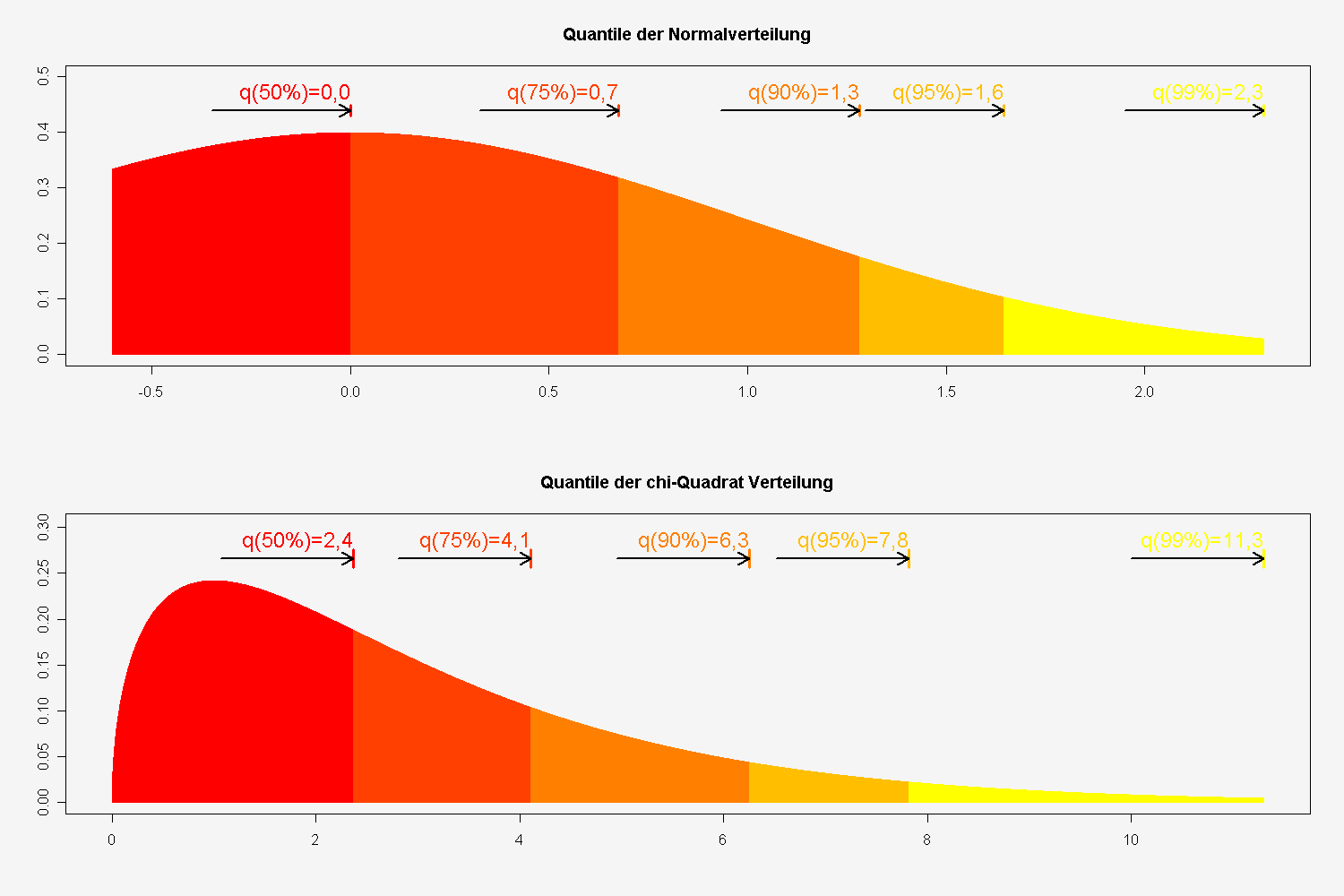
Da sich nicht einfach aufleiten lässt, arbeitet man oft mit der funktion.

Die standardnormalverteilung muss um den faktor gestreckt werden.
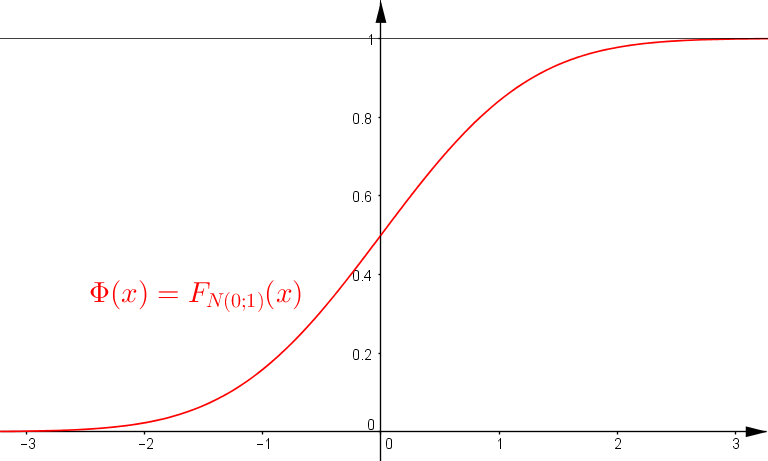
Ihr verlauf ist nebenstehend graphisch dargestellt.

Nullstellen ganzrationaler funktionen (dritten und höheren grades).
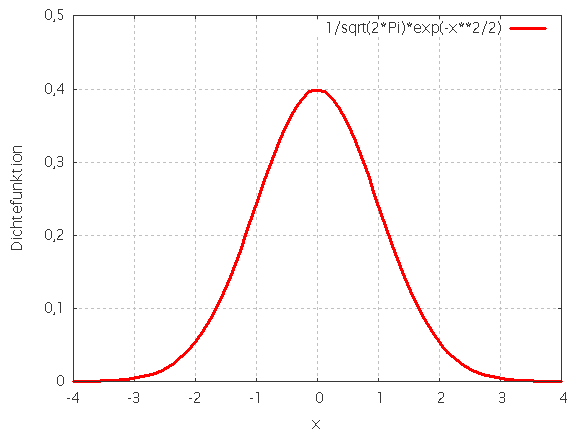
Die normalverteilung oder gaußsche verteilung ist eine stetige verteilung und hat den erwartungswert μ und die varianz ,σ2 als parameter.

Im graphen rechts ist die funktion der standardnormalverteilung abgebildet.
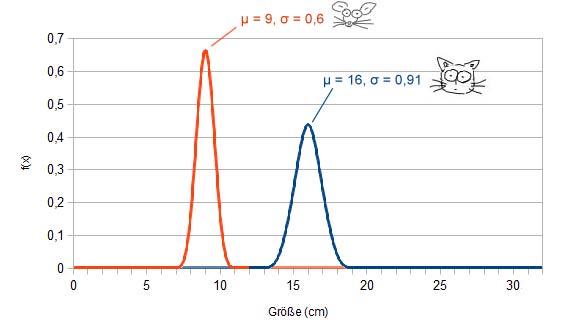
Als approximation der binomialverteilung »die näherungsfläche »die transformation in die standardnormalverteilung »beispiele »anmerkungen.
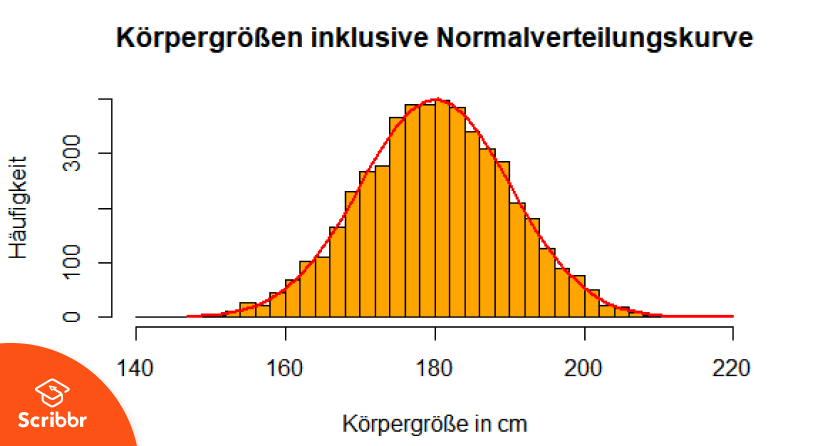
Ihr verlauf ist nebenstehend graphisch dargestellt.
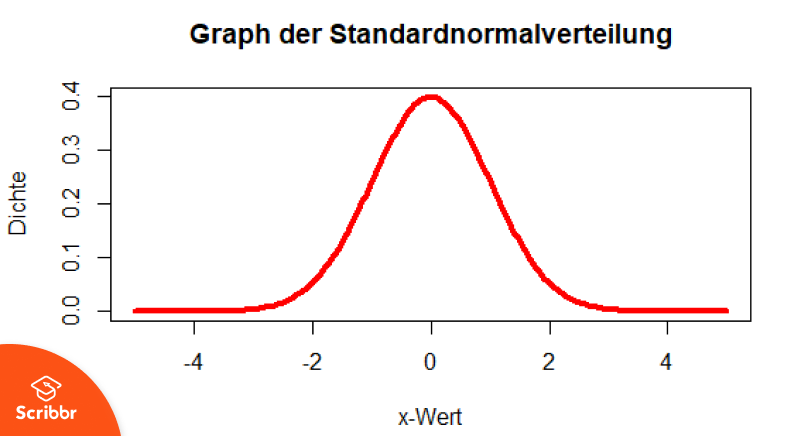
Da sich das integral der standardnormalverteilung.



